The World Is Unfair But Then Again It Is Unfair for Everyone and That Makes It Fair

Ane Thousand is Unfair, Two Thousand is Fair

Everyone speaks about the conditions, but nobody does anything nigh it. Sure unfairnesses of the earth tin all the same occasionally be pointed to, then formulated via crisp questions, then addressed and analysed, and in rare cases such efforts might even contribute to irresolute the globe. In 1994 I published a written report about a certain indicate estimate being 0.06 seconds, which then changed the Olympics; since Nagano 1998, the dart speedskaters accept had to run the 500 m twice (instead of only once). But the Olympic Unfairness Parameter is bigger for the thou m, then I'one thousand humbly asking for the Winter Olympics to alter its speedskating rules, once again.

^{Feeling the Force of the mv^ii/r formula: Kjeld Nuis & Vincent de Haître fight information technology out on the 1k.}

The Olympic 500-m and 1000-m sprint competitions are the Formula One events of speedskating, watched by millions on television forth with the fans in the stands. The athletes skate in pairs, in inner and outer lanes, switching lanes on the exchange part of the track; encounter the figure below. They attain phenomenal speeds of up to sixty km/h and naturally experience difficulties negotiating the curves, which have radii of ca. 25 m and ca. 29 m. Feel free to endeavor it yourself, at the nearest Olympic rink; at any rate you lot may outset by putting in your own weight $m$ then compute the centripetal strength of acceleration $mv^2/r$ with speed $5=15\,{g/s}$ (15 metres! per 2nd!), during the outer plough (ouch) and then during the inner turn (double-ouch).

The 500-m race: last inner vs. last outer

For the 500-m (one lap + 100 m), which takes a peak male athlete less than 34.5 seconds and the best female skaters less than 37.0 seconds, the concluding inner turn is typically the about difficult part of the race, as this book excerpt (from Bjørnsen, 1963, p. 115, and in my translation) testifies:

He drew lane with broken-hearted considerateness – and could not conceal his thwarting: First outer lane! He threw his blueish cap on the ice with a resigned motion, simply speedily contained himself and picked information technology up once again. With a offset in inner lane he could have ready a world record, perhaps be the first man in the world under forty seconds. Now the record was hanging past a thin thread – perhaps the gold medal too. At any rate he couldn't tolerate any further mishaps.

^{Евгений Гришин, four-time Olympic winner, and world record holder for the thousand 1000 from 1955 to 1966. One of his other books has the Kierkegaard title "Ili-ili".}

The trouble, for Yevgeny Grishin and the other sprinters, is that of the centrifugal forces (cf. the dispatch formula $a = mv^ii/r$) and meeting such challenges precisely when fatigue starts to kick in, making skaters unable to follow the designated curve and in effect skating a few metres extra. The Grishin extract also points to the fact that luck can take something to exercise with one'south event; for the 500 m many skaters prefer the final outer lane (that is, starting in the inner) to the terminal inner lane (starting in the outer). Thus the Olympic 500-chiliad event has carried a certain random element of potential unfairness to it, as a random draw determined whether a skater should have final inner or last outer lane. Via valiant statistical efforts I was then able to demonstrate, in a 1994 report, that the difference between last inner and last outer is statistically and Olympically pregnant, to the tune of ca. 0.06 seconds (enough of a difference to brand medals alter necks). Attributable in part to these efforts and detailed reporting, along with careful deliberation and negotiations within the International Skating Union (ISU) and the International Olympic Commission (IOC), these Olympic all-on-one-bill of fare rules were finally inverse. From 1998 Nagano onwards, the skaters have needed to race the 500-m twice, with one starting time in inner and 1 in outer lane, and with the sum of their times determining medals and the terminal ranking.

The g-m race: 3 inners + ii outers vs. ii inners + iii outers

This blog post is most the 1000-m, however. The 2-and-a-one-half-lap race looks more than asymmetric than the 500-m. If you beginning in inner, you'll have in in out out in before you cross the finishing line, whereas your compatriot in the race will accept out out in in out. The speed is even college than in a 500-1000 race; 34.00 might give you Olympic gold, just ten skaters might be improve than 1:08.00. This may sound odd, just is due to the flight start effect; top skaters demand a fleck of fourth dimension and a good stretch in front of them to get to maximum speed (and yous don't demand to start all over once more afterwards 505 metres of your m-thou race). Thus the inner guy has perhaps a slight reward in the showtime, with a longer straight stretch earlier striking the curve. Nosotros'll soon plenty wait at data and models and the (tiny) differences between inners and outers, but some other inner-factor that favours some skaters (though not all) is that when fatigue sets in and all your muscles shriek for an easier ride through the troubled agonized turn, then inner might be better for y'all.

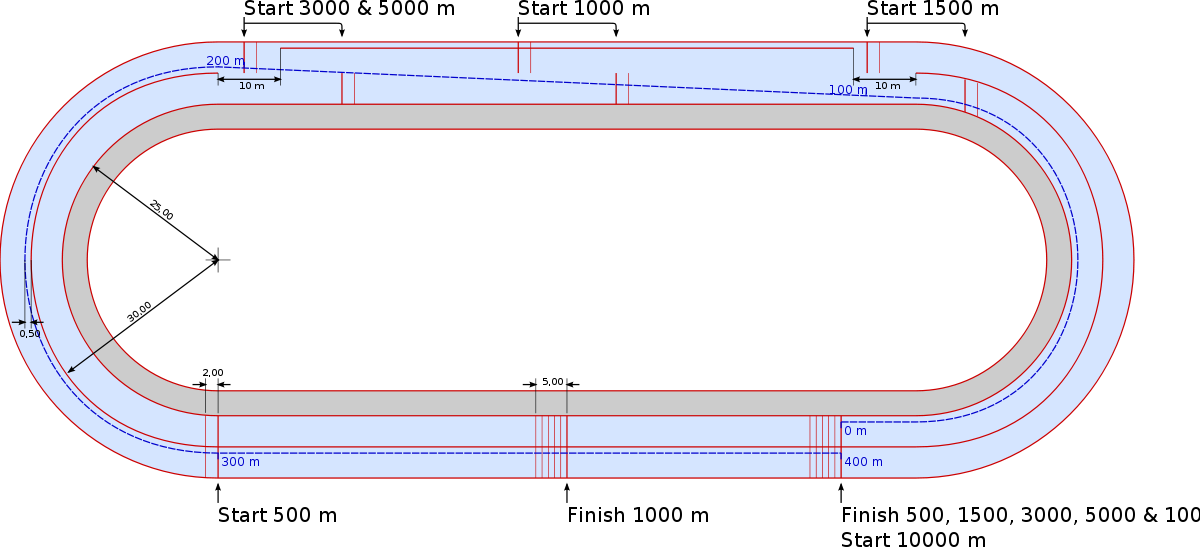
^{Higher geometry: Think through your two-and-a-half-lap race, if y'all start in inner lane (so ending in inner lane as well), or in outer lane.}

So, though an Olympic or World Title 1k certainly tin can exist won past a elevation skater starting in the outer lane, many prefer and hope for beingness blest by starting in the inner lane. That's the Burning Olympic Flame Question I'll address below, whether at that place is a perhaps slight but statistically and Olympically deviation at work. In that example (well, surprise!, I program to convince you lot, below, that there is such a difference), it should not and cannot exist expected to work in the same way, for all skaters, from occasion to occasion. Rather, I'm after a statistical average-across-skaters parameter, say

\(d=\hbox{average time lost by existence outer guy compared to if you could have been inner guy},\)

which by its nature is small, i.e. close to naught (if it had not been pocket-sized, information technology would have been detected and agreed upon some xxx years ago). To make such a $d$ parameter well divers, and identifiable and estimable from data, I need relevant good-quality data, along with a proper statistical model. Again, the $d$ looks a bit counterfactual, and can't easily be assessed from results for one given race; also, its value (when I find it, below) doesn't apply to all skaters; rather, it's an average-beyond-top-skaters value (in well executed races without falls or mishaps).

In order to grasp the scale of things, where skaters run 15 metres per second and a full kilometre in 67 seconds, checking a few upshot lists shows that medals tin easily change necks with the tiniest of time adjustments. This list is from the Saturday 1k race of the World Sprint Championships in Calgary 2017 (a dataset also returned to below), with the showtime four having started in the inner, the 2 next in the outer. Then if there's a tiny inner advantage, the outer guys would take notice.

\(\eqalign{ \qquad one\ \ &{\rm i} &{\rm G\ Nuis} &ane.06.61 \cr \qquad ii\ \ &{\rm i} &{\rm V\ de Haitre} &1.06.72 \cr \qquad 3\ \ &{\rm i} &{\rm K\ Verbij} &ane.06.73 \cr \qquad 4\ \ &{\rm i} &{\rm HH\ Lorentzen} &1.07.08 \cr \qquad v\ \ &{\rm o} &{\rm North\ Ihle} &1.07.sixteen \cr \qquad half dozen\ \ &{\rm o} &{\rm J\ Garcia} &1.07.83 \cr}\)

The Almanac Earth Dart Bigaußian Fixed and Random Effects Championships

The annual World Dart Championships provide the perfect type of data I need for comparing inners with outers and for setting up good models for identifying, estimating and assessing the $d$ parameter. In these two-day races (500 + chiliad on the Saturday, and 500 + 1000 on the Dominicus), a wise ISU rule sees to it that each skater switches start-lane, from the first to the second solar day. Hence the races are symmetric and off-white; the best skaters demand to be prepared for both types of races; and no skater can complain of bad luck past the describe. Thus Håvard Holmefjord Lorentzen had i for inner on the 1st 24-hour interval and o for outer on the 2nd day, in the Calgary 2017 Globe Sprints (where he for two brief minutes held the globe record in the 4-distances sprint combination, the kickoff fourth dimension a Norwegian had managed such a feat, since 1973). Nosotros too accept passing time (and hence lap time) data, for each skater, every bit indicated below (these are the top 6 of 25 skaters with valid results on both yard metres).

\(\eqalign{ \def\two{{\rm i}} \def\oo{{\rm o}} \qquad & &{\it Saturday} & & & &{\it Sunday} \cr \qquad i &{\rm K\ Verbij} \quad &\ii &16.35 &40.96 &66.73\quad &\oo &16.50 &41.29 &67.94 \cr \qquad 2 &{\rm H\ Lorentzen} \quad &\two &16.62 &41.39 &67.08\quad &\oo &xvi.50 &41.32 &67.38 \cr \qquad 3 &{\rm One thousand\ Nuis} \quad &\2 &xvi.65 &41.09 &66.61\quad &\oo &sixteen.63 &41.13 &66.51 \cr \qquad four &{\rm R\ Mulder} \quad &\oo &16.37 &41.04 &68.07\quad &\ii &xvi.xl &41.39 &68.23 \cr \qquad 5 &{\rm M\ Poutala} \quad &\ii &16.24 &41.26 &67.96\quad &\oo &16.38 &41.17 &67.97 \cr \qquad 6 &{\rm L\ Dubreuil} \quad &\oo &16.25 &40.98 &68.07\quad &\2 &sixteen.34 &41.17 &67.77 \cr}\)

The are several statistical venues now, for coming at the $d$ parameter, the simplest of which might be to compare the 25 results with inner (mean 1:08.27) with the 25 results with outer (hateful 1:08.51); yes, in that location appears to be a 0.24 sec advantage for inner, but the standard error we need to separate with, to bear out a unproblematic t-test, is 0.26, so the t ratio is merely 0.91, and not significant. A more informative assay is by regressing the result differences, say $y_2-y_1$ for Sunday minus Sabbatum, on the inner-outer covariate, and perhaps a few more. This is proving more than valuable, and gives a clear, pregnant $d$ in favour of the inner.

Nosotros may practise better, nevertheless, past building a coherent statistical model for the $(y_1,y_2)$, incorporating all relevant information, from 200- and 600-passing times to the variability structure (which should comprehend both day-to-solar day variation and skater-to-skater variation), and, crucially, the inner-outer-information. My considered model takes this form, for 1st race and 2nd race results $(y_{i,i},y_{i,ii})$ for skater no. $i$:

\(\eqalign{ y_{i,1}&=a_1 + bu_{i,ane}+cv_{i,i}+\hbox{$1\over2$}dz_{i,1} +\delta_i+\varepsilon_{i,i}, \cr y_{i,ii}&=a_2 + bu_{i,ii}+cv_{i,2}+\hbox{$1\over2$}dz_{i,2} +\delta_i+\varepsilon_{i,two}, \cr}\)

with $(u_{i,1},u_{i,2})$ passing times after 200 m, $(v_{i,1},v_{i,2})$ passing times later 600 m; $\delta_i$ a parameter post-obit skater $i$, modelled as from a ${\rm N}(0,\kappa^2)$ distribution, and $(\varepsilon_{i,ane},\varepsilon_{i,two})$ are independent error terms, from a ${\rm Northward}(0,\sigma^2)$ distribution. Crucially, the inner-outer data is taken care of via $(z_{i,1},z_{i,2})$, with $z=-1$ if commencement in inner and $z=1$ if start in outer. If $d=0.12$, for case, it means a fourth dimension adjustment of $-0.06$ seconds for the inner guy (good) just $+0.06$ for the outer guy (bad).

The race-to-race variation is in the $\varepsilon_{i,j}$, identified with the $\sigma$, whereas the skater-to-skater variation is in the $\delta_i$, identified with the $\kappa$. A splendid skater has a negative $\delta_i$ (and a not-and so-first-class skater has a positive $\delta_i$), though we practice not attempt to approximate information technology direct, for each skater, simply through the variation amid skaters. I have as well slightly modified the variables here, to subtract overall means of $u_{i,1}$ and $u_{i,2}$ in their definitions, and similarly for the $v_{i,ane}$ and $v_{i,2}$; this eases interpretation and also helps stabilise numerics. In particular, $a_1$ and $a_2$ may now be seen as the overall expected levels on the 1st and second day of the competitions. Parameter $b,c,d$ are regression structure parameters, signalling the outcome of $u$ and $v$ and $z$ on the overall results, whereas $\kappa$ and $\sigma$ relate to variability and inter-skater correlation.

The model has both fixed effects, related to the $a_1, a_2, b, c, d$ parameters, and random effects, via the skater-parameter $\delta_i$. I utilize $a_1$ for race 1 and $a_2$ for race 2, since racing conditions might differ, in terms of temperature, humidity, etc. (and current of air, if outdoor). The model thus have vii parameters, and may also be represented every bit

\(y_i=\pmatrix{y_{i,1} \cr y_{i,2} \cr} \sim{{\rm N}}_2(X_i\pmatrix{a_1 \cr a_2 \cr b \cr c \cr d \cr}, \pmatrix{\sigma^2+\kappa^2 & \kappa^2 \cr \kappa^2 &\sigma^two+\kappa^2 \cr}), \)

for skaters $i=1,\ldots,n$, with the appropriate $2\times5$ covariate matrix $X_i$. Given the combined considerable efforts of the 25 skaters sprinting away in Calgary, World Dart 2017, I tin now fit and appraise the model, and, in particular larn whether the globe was unfair then, by seeing if $d$ was close to cipher or not.

Estimating and assessing the Olympic Unfairness Parameter

I do not get into the technical details here, but given the data and the model I've built in a higher place, I can apply statistical methodology to

• (i) fit the model, i.e. estimate regression parameters $a_1,a_2,b,c,d$ and variance parameters $\sigma,\kappa$;
• (ii) assess the relevant uncertainty, in particular setting upward standard errors and say 95% conviction intervals;
• (iii) screen out whatever outliers (and I practise non wish an accidental mishap for one or two of the skaters to mess upwards the analysis and the conclusions):
• (iv) assess the full fit of the model.

Formulae and derivations and details and relevant give-and-take can exist found in the Schweder and Hjort CLP book (2016, Ch 14). The basic estimation method is that of maximum likelihood, along with formulae for variance matrices, etc. Also, various model adequacy checks pan out very well (after careful screening abroad of outliers).

Note here that even though we might only treat $d$, the unfairness parameter, it is part and bargain of the statistical modelling and methods that I somehow demand to cistron in the other six parameters also (there's no gratuitous cake mode of finding $d$ directly). For Calgary Globe Sprint 2017 I find $\widehat d=0.282$ seconds, a rather drastic estimate for the unfairness parameter, with estimated standard deviation 0.102. This translates to a t ratio of 2.776, a p-value for testing fairness ($d=0$) of 0.003, and a 95% confidence interval of $[0.083,0.481]$.

This is already pretty disarming, only cannot be taken at statistical trust value but nonetheless, since this estimate, though meaning and worrisomely big, has been obtained for just one World Dart, that of 2017; this is also reflected in a rather wide conviction interval. The standard errors go down like $ane/\sqrt{n}$, with $n$ the number of skaters, and then we need more volunteers, among the height dart skaters of the world, to give us more than lovely races and hence increased statistical precision. The analysis is strengthened, considerably, past going through several Earth Sprint events. I have done so, for a list of such events, and volition here briefly summarise results for the ten last Globe Sprint Championships, from 2017 backwards in fourth dimension to 2008.

Displayed in this figure are indicate estimates $\widehat d_j$ (ruddy dots), event by event, for the underlying unfairness parameters $d_j$, from Heerenveen 2008 to Calgary 2017. I also give 95% confidence intervals for each outcome, based on the statistical machineries of models, probability calculations, and data. The overall motion-picture show is pretty convincing; fairness would hateful that the zero line $d=0$ should be covered by these intervals, for most of the events, and clearly it is not.

A fuller analysis is pointed to below, with a configram constructed for ten individual conviction curves, i such ${\rm cc}(d_j)$ for each of the World Sprint events, along with a bigger and fatter overall confidence curve, say ${\rm cc}^*(d_0)$, for the overall unfairness parameter $d_0$. This is the more narrow confidence curve in the middle, pointing to the grand overall estimate $\widehat d_0=0.187$ seconds. A 99% confidence interval for this overall $d_0$ is found to be $[0.108,0.266]$. I go out out the technical details hither, only I'm following the general meta-assay methods for such setups, in Schweder and Hjort (2016, Ch. 13). 1 ingredient here is to model the events, from 2008 to 2017 and beyond, not to accept the exactly same unfairness parameter value, as these may vary, slightly, from event to upshot; thus these are seen as $d_j\sim{\rm N}(d_0,\tau^2)$. A separate conviction distribution analysis of the spread parameter $\tau$ gives a 95% confidence interval $[0.023,0.136]$, with point gauge $\widehat\tau=0.069$.

To sum up, translating from statistics to speedskating, these analyses propose the post-obit.

• (i) Each World Sprint event has its own unfairness parameter, say $d$, which may vary from occasion to occasion, inside the band from a slim 0.058 seconds (about fair) to 0.316 seconds (very imbalanced).
• (ii) The overall unfairness judge is 0.187 seconds. It is highly pregnant, and the associated 99% confidence interval is very clearly to the correct of cypher, hence favouring the inner guy.
• (iii) The world becomes more fair (and a better one) when skaters are turning in two 1000-yard races, one with start in inner and one with start in outer (and with the sum of the two race times determining the final result listing). The start list for the 2nd race would then be the 1st race result list turned upside down, with a natural crescendo towards the all-time skaters well-nigh the end, and with each new pair, and the public, knowing precisely what is required to atomic number 82 in the point-sum. This would exist similar to what is in place for alpine skiing, for skijumping, and notwithstanding other sports. This kind of arrangement is already in place for the annual World Dart Championships, only not for the Olympics, and not in the almanac World Single Distances Championships.

Notes & Concluding Remarks

Readers of my papers, over the years, whether about methodology or applications, have perhaps grown accustomed to a final section where I insist upon giving some "final remarks, some of which point to further research" (well, in cases where the periodical editors have granted me this opportunity). Speedskating stories should not exist exempt from this habit, so here I go.

A. What is information technology well-nigh speedskating that could bring an entire people together around the radio or television, women and men, young and old, rich and poor? What was it that compelled children to scribble down skate times and collect them in books? Why are the names of Kay Stenshjemmet, January Egil Storholt, Sten Stensen and Amund Sjøbrend etched in my memory 40 years after they hung up their skates for practiced, whereas I have long since forgotten the names of prominent politicians of the 24-hour interval or the teachers I had at school? – These thoughts are admittedly penned by Knausgård (Feb 2018), but they echo my own, and those of long generations of Norwegians. "It is when this struggle becomes plain that speedskating goes from sport to drama. Abruptly, the skater's fatigued-out inner battle becomes visibly external, will confronting torso, torso against clock, played out before thousands of eyes, transforming the last throes of the struggle against the body into a struggle confronting humiliation, against no longer remaining together, no longer being elegant, no longer being able to skate." Knausgård explains, to a few million culturally challenged Americans and others, that the signal is not to win, but to struggle, to win with suffering (whether over yourself or your competitors).

These puritan, solitary, half-invisible aspects of speedskating are too fabricated clearer in a glorious twelve-folio photo essay about Redningsskøytene (also from February 2018), in Dagens Næringsliv'southward D2 Magazine. These dimensions are certainly present, when i hopes to explain or understand why the mysterious and partly introverted world of speedskating is so prominently at work, even on the pages of the nation's nigh serious novelists. I'd like to point out one more of these dimensions, though, regarding the Fields of Attraction: Statistics. Perhaps Northward Americans swallow baseball game statistics and batting averages for breakfast. A couple of generations of Norwegians learned numbers and calculus and statistics from speedskating. How should a proper 1500 m be prepare up, with which 3 laptimes following the 300-k opener, for a long-distance guy to optimise his chances of getting a bronze in the weighted-pointsum competition, given that he won the argent on the 5k and that his main opponent for said bronze, the 1500-thousand specialist, just did i:46? 28000 Bislettians would quickly take done the maths and the stats and the predictions. Svein Sjøberg, professor of physics and of didactical learning for the sciences, who oft laments the land of the nation when it comes to basic knowledge of maths and sciences (and who skated against Fred Anton Maier in the 7.28.i March 1965 race, and against Jonny Nilsson in the 4.27.6 March 1963 race, as we all call up), says said nation needs to learn more of the basics, from, well, speedskating.

B. Essentially the aforementioned ii 10 1000 thou story has been written upward as part of the Application Chapter 14 in Schweder and Hjort's 2016 CLP book (with sprint data up to 2014, whereas this weblog mail has been using such data besides from seasons 2015, 2016, 2017), with some more details regarding the mathematics of the confidence distributions and configrams. I've also communicated the essential Olympic Unfairness findings to the ISU.

C. When I wrote up my Olympics-Changing 1994 study, the cyberspace wasn't fully invented yet, and I needed hard copies of all ISU result protocols to painstakingly put all inner-outer and lap fourth dimension information into my files. Such information-gathering and file-organisational efforts are often enough part of the statistician'south work tasks, also now. In 2018 it's relatively easy for me to find the relevant information, from ISU Results websites, simply I still demand an extra 25 minutes per World Dart event to transform and interpret and mail service-edit just the right information in just the correct format (unless I devise a improve net-scraping algorithm, which I haven't attempted), followed by careful outlier monitoring.

D. Given my bigaussian fixed-and-random furnishings model above, I tin bypass some of the log-likelihood part complexities and work with a simpler regression model for the differences $D_i=y_{i,2}-y_{i,ane}$ in terms of laptimes and the inner-outer covariate. This leads to a competing reckoner, say $\widehat d_{\rm simple}$, which is typically merely slightly less precise than my preferred $\widehat d_{\rm bigmodel}$ used higher up. The results coming out of such procedures are largely similar to those exposited to a higher place. I do adopt the total bivariate model, still, as well since it provides other relevant information for the eager observer of speedskating, similar the skater-to-skater and the inter-skater day-to-day variability, the upshot of preliminary passing times on the final results, etc. In Hjort, Dahl, Steinbakk (2006), apropos, we spend quite a flake of time studying the intricate correlation structure for sets of 500-k and grand-yard results.

East. The analyses given hither have neutrally but finer pointed to and assessed the unfairness, without necessarily giving precise "but why?" explanations for the observed inner-advantage. Plausible reasons include those briefly mentioned, (i) the inner guy has a longer straight-ahead stretch to build speed at the start; (ii) the sprinters who use all their sprinting forces to have maximum speed for 900 grand and so promise for the best for the remaining 100 1000 accept clear difficulties with the last outer lane, when fatigue sets in and your muscles are called-for and your body is close to the Knausgårdean collapse. There is a third reason favouring last inner, all the same, which I haven't attempted to analyse hither, having to do with air resistance and the eating up your pairmate phenomenon on the final commutation stretch. Erben Wennemars and others brand the point that if the two skaters are pretty shut with one lap to go, so the concluding inner guy will win – really with an boilerplate fourth dimension advantage of 0.67 seconds, for that terminal lap alone (they appear to claim). Famously, you tin't really programme to have luck with your partner in life, as information technology depends on how the partner behaves in the course of the life I mean race. But it'due south i more than good reason for demanding 2 x 1000 thousand, with one start in inner and i in outer.

F. The speedskating world has changed in several ways over the past 20-25 years (some would say far too much). In addition to the traditional distances 500-m, 1000-m, 1500-m, 5k, 10k for men (and 500-g, one thousand-yard, 1500-grand, 3k, 5k for ladies), there is now the team race (three skaters on a team, over eight laps, only inners, pursuing the team on the other side of the rink), mass start, and fifty-fifty three-leg-catapult-sprint. This means more events inside a crowded Olympic or World Championships time window, which also leads to a pressure of having fewer races. Thus the two x 500 thousand setup has been left, confronting the protest of many skaters, for the Olympics and also for the Earth Unmarried Distances Championships; the 2 x 500-thousand plus 2 x thou-m setup of things, is still being kept for the Earth Sprints, notwithstanding. The implication is that fifty-fifty if skaters and specialists agree with me (and virtually do), it'll be hard to squeeze in another 1000-m for the Olympics.

G. Several Olympic and World Championships 1000-k and 500-1000 winners have published books well-nigh their lives and careers (or have had journalists writing nearly them), among them Dan Jansen, Catriona LeMay Doan (whose honour I once had to defend, in Aftenposten, after that newspaper's sexist nakendamehartkornslåingoppslag most her – " Det er her jeg må trekke paw slitte riddersverd, i erkjennelse av at landets militante feminister sannsynligvis har måttet gi opp sin interesse for hurtigløp på skøyter etter den stemoderlige behandling denne idrett nå har i media. Avsnittet over er nemlig grovt feilaktig og krenkende."), Yevgeny Grishin, Erhard Keller, Peter Mueller, Annie Friesinger, Eric Heiden. They all make comments near the inherent dangers of the outer lane in the 1k. Dianne Holum (1984, p. 225), for case, rather clearly blames starting in the outer on her Sunday-m-m for losing the 1972 World Championships to Monika Pflug.

H. The model I've built and used for these analyses is moderately complicated by having fixed and random effects, and I've worked out estimation and assessment methods and algorithms from scratch, so so speak. The model is however besides a special instance of the so-called linear mixed models, for which methodology and R packages accept been worked out, from general perspectives. See as well the FIC for Whales work, where Céline Cunen, Lars Walløe and I hammer out new methods and formulae for model selection and model assessment, for these classes of models, and where the FIC machinery we develop may be applied also for the Earth Dart Championships data.

Thanks

I am grateful to all the participants of these ten years of annual World Sprint Bigaußian Fixed and Random Furnishings Championships, for their spellbinding & mindboggling efforts, which continue to be a joy to behold. I also give thanks Céline Cunen and the others at the FocuStat research group for discussions of several of the pertinent methodological points, and also the multitude of eager contributors of cognition and tireless discussants of all historical matters, small and large, in the vibrant and broadminded Forum for Skøytehistorie on Facebook.

References

Bjørnsen, K. 13 år med Kuppern & Co. Nasjonalforlaget, Oslo.

Cunen, C., Walløe, L. and Hjort, N.L. (2018). Focused model selection for linear mixed models, with an application to whale ecology. (Submitted for publication, February 2018.)

Friesinger, A. Mein Leben, mein Sport, meine besten Fitness-Tipps. Goldmann, Berlin.

Гришин, Е.Р. (1969). 500 метров. Publisher: Молодая гвардия.

Gundersen, J.-A.Ø. (2018). Redningsskøytene. 12-page report and essay on the new wave of Norwegian peak skaters, in Dagens Nærlingslivs D2 magasin.

Heiden, E. (1979). For moro skyld. Cappelen, Oslo.

Hjort, N.Fifty. (1994). Should the Olympic speed skaters run the 500 m twice? Statistical Research Written report, Section of Mathematics, Academy of Oslo.

Hjort, N.L., Dahl, F.A. and Steinbakk, G.H. (2006). Post-processing posterior predictive p-values. Periodical of the American Statistical Association 101, 1157-1174.

Holum, D. (1984). The Consummate Handbook of Speed Skating. High Peaks Cyclery, Lake Placid.

ISU Results (International Skating Matrimony). Results from international championships, in item from the World Sprint Championships, can exist establish here, for the 2017 upshot used to a higher place, and here, for other seasons (before long to include the 2018 Olympics and the March 2018 Changchun World Sprint).

Jansen, D. (1994). Total Circumvolve. Villard Books, New York.

Keller, Eastward. (1968). 74 Schritte zum Ziel. Copress-Verlag München.

Knausgård, One thousand.O. (2018). The Hidden Drama of Speedskating. Essay, The New York Times, one-Feb-2018.

LeMay Doan, C. (2002). Going for Gold. McClelland & Stewart, Toronto.

Rosa, D. and Hjort, N.L. (1999). Who Won? The Annual Speedskating Race of the Burg of Ducks. Speedskating World. (Also included in Don Rosa Collected Works, 2011.)

Scholten, Thou. (2005). Op dun ijs - Het verhaal van Peter Mueller. Arko Sports Media Bv, Amsterdam.

Schweder, T. and Hjort, Due north.L. (2016). Confidence, Likelihood, Probability: Statistical Inference With Confidence Distributions. Cambridge University Press, Cambridge.

Wennemars, Due east. (2017). Wennemars legt uit: het geheim van de binnenboch. The multiple World Sprint Champion gives a pedagogical idiot box lecture (which for educational reasons, I suppose, lasts precisely every bit long as Grishin's 1955 earth record fourth dimension for the 1k) to the Dutch about The Secret of the inner lane.

Published Feb. 5, 2018 9:xviii PM - Final modified Nov. 13, 2020 11:14 AM

wigginsnellootiout57.blogspot.com

Source: https://www.mn.uio.no/math/english/research/projects/focustat/the-focustat-blog%21/twotimesthousand.html

Bagikan Artikel ini